Teorema del punto gordo

Demostración a la española

¡Qué puntazo!

— Miguel de Cervantes sobre el Teorema del Punto Gordo

"Y en un principio.. toda la materia y energía estaba concentrada en un punto... solo que ese punto era muy gordo... Muy muy gordo... de hecho...creo que todavía hoy sigue concentrada en ese punto"

— Stephen Hawking sobre el Teorema del Punto Gordo

¡Oh! el teorema del punto gordo, me fue muy útil en la construcción de la torre de pisa.

— Eiffel sobre el Teorema del Punto Gordo

El teorema del punto gordo (TPG de aquí en adelante) sostiene que dos rectas paralelas se cortan en un punto, siempre que el punto sea suficientemente gordo.

Cabe destacar que el origen del revolucionario teorema es español.

Versión matemático-freak

Demostración friki-matemática

Obviamente, este hallazgo de origen soriano supuso una grave ofensa a la comunidad freak y a la comunidad matemática (se rumorea que ambas son la misma), aunque con el tiempo no tuvieron más que aceptar el teorema. No obstante, reescribieron el hallazgo:

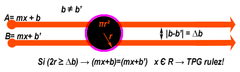
Sean A y B dos funciones de primer grado f(x)=mx+b cuyas derivadas sean iguales f'(A)=f'(B), y con término independiente b desigual en la función primitiva; se cumple el teorema del punto gordo cuando el doble del radio r de dicho punto es mayor o igual que la diferencia de los términos independientes de las rectas A y B. Se considera que el citado punto es suficientemente gordo cuando el doble de su radio es mayor o igual a la adición de los términos independientes, siendo igual válido a radios mayores al planteado.

Por lo tanto, se sabe que ambas rectas se cortan en un punto x, por el cual:

(A=mx+b)=(B=mx+b'), para x ∈ R; y b≠b' → mx+b=mx+b' → mx-mx+b=b' → 0=b'-b → b=b'

Lo cual niega la premisa inicial b≠b' y demuestra que Soria sufre un extraño campo magnético que ocasiona que las leyes matemáticas no se cumplan en dicho país europeo.

Corolario: El punto gordo y la intersección de tres rectas

Tres rectas (no necesariamente paralelas) se intersecan en un punto, si este es un punto suficientemente gordo.

Corolario II: El Punto gordo y la Recta Astuta

Una recta pasa por tres puntos no alineados, siempre que al menos uno de los puntos sea lo suficientemente gordo o la recta lo suficientemente astuta.

Corolario III: Paralela por un punto

Por un punto exterior a una recta puede trazarse una paralela y solo una, excepto si el punto es gordo que pueden trazarse muchas.

Extensión del Teorema: El punto movido

Este teorema es útil cuando se intenta demostrar teoremas referidos a gráficas, como pueden ser los polinomios interpoladores, mínimos, máximos, puntos de inflexión, etc.

La base de este teorema se trata de economizar el trazado de puntos, y este es:

Dibujados ciertos puntos (x_i,y_i), si este punto no converge a la gráfica, el coste de redibujar dicho punto sobre la gráfica es menor que el de redibujar la gráfica para que esta converja al punto.

Generalización de McGyver para el corolario de las tres rectas

Sea n un número natural y sean r₁, r₂, ... r_n, n rectas cualesquiera. Existe, por lo menos, un punto gordo en el que se intersectan las n rectas, dicho punto puede construirse con chicle, un balde de agua, dos elasticos, un poco de tierra, estiercol de murcielago y la gracia de Monesvol.

Dem.

Es fácil de hacer, por inducción sobre n y mucho chicle.

Principales utilidades del Teorema

Este teorema y sus corolarios presentan grandes avances para la humanidad en general, entre los que cabe destacar:

• Poder juntar en medio de un examen de dibujo técnico en un punto gordo tres o más líneas que deberían de juntarse en un punto común pero que, aún habiendo seguido el procedimiento a la perfección y con total precisión, por alguna razón cada una cruza por donde le sale de los cojones.

• Ya no es necesario imaginarnos cosas raras como "el punto al infinito" de la proyección perspectiva. Ahora sabemos que dos paralelas realmente se juntan en (por lo menos) un punto gordo.

• Los políticos lo aplican en su quehacer cotidiano, así pueden afirmar que el crecimiento durante su reinado mandato ha sido, por ejemplo, del quince por ciento menstrual de manera sostenida, sin importar que dicho crecimiento haya sido negativo, basta con que la gráfica de crecimiento use rectas formadas únicamente por puntos gordos

Enlaces externos

• La comunidad de Menéame, se congratula ante semejante hallazgo soriano, demostrando la indiscutible seriedad de la Inciclopedia.